Table of Contents
Introduction
Language used: R (Markov Chains package)
Task to solve: Analyze the Bad Payers situation.
Transitional matrix with this components:
Group A (good payers)
- 30% will stay in this category
- 30% will become a bad payer (Group B)
- The rest will pay all overdue
Group B (bad payers)
- 10% goes to the default stage
- 20% pays the overdue
- 40% will stay in Group B
- 30% will go to Group A
D (default): Default
P (pagado): Paid
Markov Chain
Transitional Matrix
The states D and P are absorbing states.
Probability D P A 0.09 0.91 B 0.21 0.79
Additional Limits:
| Investment type | Investment out of all funds | |
|---|---|---|
| Consumer credit | Maximum 15% | |
| Housing loans & Gold deposits | Minimum 5% |
Mathematical Model
Decision Variables:
- Consumer credit
- Corporative bonds
- Gold deposits
- Housing loans
Function to maximize the earnings Z=0.07*x1+0.11*x2+0.19*x3+0.12*x4
Limits
- x1+x2+x3+x4=5
- x1<=1
- x2<=1.5
- x3<=2.5
- x4<=1.7
- x3+x4>=0.05(x1+x2+x3+x4)
- x1<=0.15(x1+x2+x3+x4)
Solution
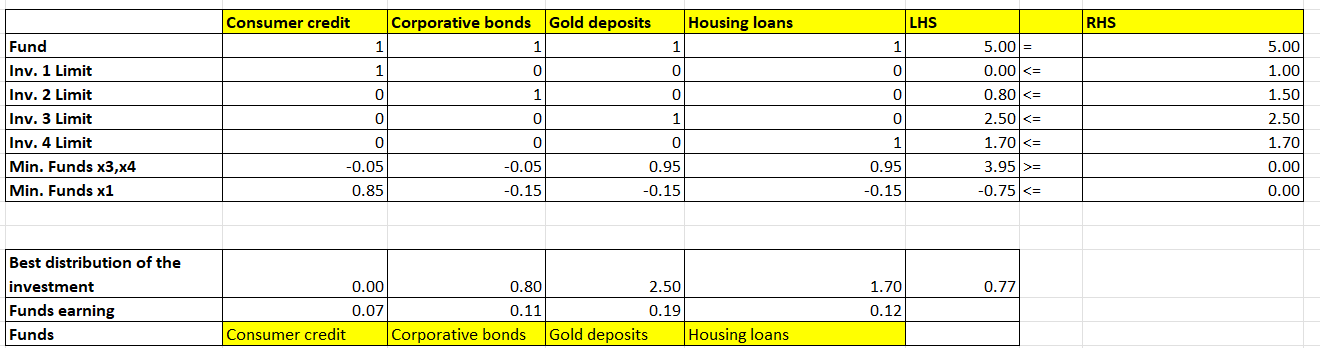
Best distribution of the investment
Starting Fund to invest: $5.000.000,00
| Type of investment | Amount of investment ($) | Percentage of the total earnings |
|---|---|---|
| Consumer credit: | 0 | 0,00% |
| Corporative bonds | 800.000,00 | 16,00% |
| Gold deposits | 2.500.000,00 | 50,00% |
| Housing loans | 1.700.000,00 | 34,00% |
| Earning to be achieved (per year) as per calculations |
|---|
| $ 767.000,00 - 15,34% of the starting investment |